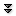$\def\puz{\mathop{\strut\mathrm{puz}}}$
The well-known 15-puzzle consists of 15 sliding squares in a $4\times 4$ grid. The object is typically to return a scrambled puzzle to the configuration shown below, or to produce some other specified pattern from this configuration.
scramble | reset
A legal move in the puzzle consists of sliding a square into the blank spot; click on the square you want to move. The original version of the puzzle above can be found at Archimedes' Laboratory.
Viewed as a permuation of 16 items (the 15 squares plus the blank spot), this is the transposition of the blank with another item. If the blank spot is returned to the bottom right corner after a series of such moves, the number of moves must be even, and hence any pattern produced in this way must be an even permutation. For example, we cannot produce the pattern in which the 14 and 15 squares are interchanged and all other squares remain in their original places, since that is an odd permutation. This leaves open the question of whether all even permutations can be produced by a sequence of legal moves; as we will show, the answer is yes. Our proof is essentially that of Aaron Archer .
We begin by relabeling the puzzle pieces for convenience:
The new numbering follows the path shown by dashed lines. We now want to show that all even permutations of this starting configuration can be achieved.
We define nine simple permutations that can be achieved as follows: for each, swap the blank along the dashed path until arriving at one of the squares 6, 8, 10, 12, 14, 16 (the bottom right square, that is, the blank doesn't move at all). Now swap the blank up, then swap it along the dashed path back to its original position. For example, if we stop at square 12 we get this:
In this permuation, 1 through 4 and 12 through 15 are in their original positions. The permutation is a single odd cycle, $(11,10,9,8,7,6,5)$. In the same way we produce 5 other cycles: $$\eqalign{ p_1&=(5,4,3)\cr p_2&=(7,6,5,4,3,2,1)\cr p_3&=(9,8,7)\cr p_4&=(11,10,9,8,7,6,5)\cr p_5&=(13,12,11)\cr p_6&=(15,14,13,12,11,10,9)\cr }$$ Now we note that $$\eqalign{ p_2^{2}p_1^2p_2^{-2}&=(1,2,3)\cr p_2^{1}p_1^2p_2^{-1}&=(2,3,4)\cr p_1^2&=(3,4,5)\cr p_2^{-1}p_1^2p_2^{1}&=(4,5,6)\cr p_4^{2}p_3^2p_4^{-2}&=(5,6,7)\cr p_4^{1}p_3^2p_4^{-1}&=(6,7,8)\cr p_3^2&=(7,8,9)\cr p_4^{-1}p_3^2p_4^{1}&=(8,9,10)\cr p_6^{2}p_5^2p_6^{-2}&=(9,10,11)\cr p_6^{1}p_5^2p_6^{-1}&=(10,11,12)\cr p_5^2&=(11,12,13)\cr p_6^{-1}p_5^2p_6^{1}&=(12,13,14)\cr p_6^{-2}p_5^2p_6^{2}&=(13,14,15)\cr }$$ Thus, we can produce any $3$-cycle of the form $(i,i+1,i+2)$. You can use Sage to verify these products. Note that Sage evaluates products of permutations from left to right, so the products above are entered in the reverse order. Now a lemma and a theorem will finish things off.
Lemma 1.0.1 The 3-cycles of the form $(i,i+1,i+2)$ in $S_n$ generate all of the 3-cycles in $S_n$.
Proof. The proof is by induction on $n$. The base case is $n=3$. $S_3$ contains just two 3-cycles, $(1,2,3)$ and $(1,3,2)$. Since $(1,3,2)=(1,2,3)^2$, we're done.
Now suppose $n\ge 4$. We have 3-cycles $(1,2,3),(2,3,4),…,(n-3,n-2,n-1),(n-2,n-1,n)$. By the induction hypothesis, $(1,2,3),(2,3,4),…,(n-3,n-2,n-1)$ generates all 3-cycles in $S_{n-1}$. Also by the induction hypothesis, the cycles $(2,3,4),…,(n-3,n-2,n-1),(n-2,n-1,n)$ generate all 3-cycles in the symmetric group on the elements $\{2,3,\ldots,n\}$. Thus, we can generate all 3-cycles except possibly a 3-cycle of the form $(1,x,n)$ or $(1,n,x)=(1,x,n)^2$. Of course, if we can generate the former we can generate the latter. Let $y\notin\{1,x,n\}$. Then we know we can generate $(1,x,y)$ and $(y,x,n)$; then $(1,x,y)(y,x,n)=(1,x,n)$. This finishes the proof. $\qed$
Theorem 1.0.2 The 3-cycles in $S_n$ generate $A_n$.
Proof. Suppose $\sigma\in A_n$, so $\sigma$ is a product of an even number of transpositions: $\sigma=(a_1,b_1)(a_2,b_2)\cdots(a_k,b_k)$, with $k$ even. Consider an adjacent pair $(a_{i-1},b_{i-1})(a_i,b_i)=(a,b)(c,d)$ with $i$ even. If $\{a,b\}=\{c,d\}$ then $(a,b)(c,d)$ is the identity and trivially a product of 3-cycles. If $a=d$ and $a,b,c$ are distinct, then $(a,b)(c,a)=(a,c,b)$. Finally, if $a,b,c,d$ are distinct, $(a,b)(c,d)=(a,b,c)(b,c,d)$. Thus $\sigma$ is a product of 3-cycles. $\qed$
Putting these results together with the fact that all 3-cycles of the form $(i,i+1,i+2)$ can be realized in the 15 puzzle, we see that all even permutations can be realized.