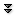Definition 1.2.1 The elementary symmetric functions in $\{x_1,\ldots,x_n\}$ are $$a_j=\sum_{X\in{[n]\choose j}} \prod_{i\in X} x_i,$$ where ${[n]\choose j}$ is the collection of all subsets of $\{1,2,\ldots,n\}$ of size $j$. In other words, $a_j$ is the sum of all possible terms formed by multiplying $j$ of the $x_i$ together. $\square$
Remark The elementary symmetric functions arise quite naturally: $$\prod_{i=1}^n (t-x_i)=t^n-a_1t^{n-1}+a_2t^{n-2}-\cdots+(-1)^na_n$$ is a polynomial with roots $x_i$.
Lemma 1.2.2 If $E$ is the splitting field for $f(x)$ over $F$, then $[E\,\colon F]\le n!$, where $n$ is the degree of $f$.
Proof. By induction on $n$. Let $b$ be a root of $f$ in $E$. Since $b$ is the root of a polynomial of degree $n$, $[F(b)\,\colon F]\le n$. Also, $(x-b)$ must divide $f(x)$ over $F(b)$, so let $g(x)=f(x)/(x-b)$. $E$ is the splitting field for $g(x)$ over $F(b)$, so by the induction hypothesis, $[E\,\colon F(b)]\le (n-1)!$. Now $$[E\,\colon F]=[E\,\colon F(b)][F(b)\,\colon F]\le n(n-1)!= n!.$$ $\qed$
Theorem 1.2.3 If $F$ is a field, $F(\bar x)$ is the field of rational functions in the variables $\bar x=\{x_1,\ldots,x_n\}$. Let $S\subseteq F(\bar x)$ be the subfield fixed by the symmetric group $S_n$, interpreted as acting on $\{x_1,\ldots,x_n\}$. Then
a. $[F(\bar x)\,\colon S]=n!$
b. $G(F(\bar x)/S)=S_n$
c. $S=F(\bar a)$
d. $F(\bar x)$ is the splitting field of some polynomial over $S$
Proof. The elementary symmetric functions $a_i$ are clearly in $S$, so $F(a_1,\ldots,a_n)\subseteq S$. The polynomial $p(t)=\prod_{i=1}^n (t-x_i)$ splits in $F(\bar x)$ and has coefficients in $F(\bar a)$, and in fact $F(\bar x)$ is the splitting field of $p(t)$, since $F(\bar x)$ is the smallest field containing all of the roots $x_i$. By the lemma, $$\eqalignno{ &[F(\bar x)\,\colon F(\bar a)]\le n!.& (1.2.1)\cr }$$ Thus, $[F(\bar x)\,\colon S]$ is finite, and since $S_n\le G(F(\bar x)/S)$, $$\eqalignno{ &[F(\bar x)\,\colon S]\ge |G(F(\bar x)/S)| \ge |S_n| = n!.& (1.2.2)\cr }$$ Combining equations 1.2.2 and 1.2.1, $$n!\ge [F(\bar x)\,\colon F(\bar a)]=[F(\bar x)\,\colon S][S\,\colon F(\bar a)]\ge n![S\,\colon F(\bar a)]\ge n!.$$ Thus $[S\,\colon F(\bar a)]=1$ so $S=F(\bar a)$, and $[F(\bar x)\,\colon S]=n!$. Now using equation 1.2.2 again, $|G(F(\bar x)/S)|=n!$, and so $G(F(\bar x)/S)=S_n$. $\qed$