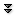Proof. Since $H$ fixes $E_H$, $H\le G(E/E_H)$. By theorem 1.1.4, $[E\,\colon E_H]\ge |G(E/E_H)| \ge |H|$. If we can show that $|H|\ge [E\,\colon E_H]$ then both (a) and (b) follow immediately.

Since $[E\,\colon E_H]< \infty$, $E=E_H(a)$ for some $a$, by the Primitive Element Theorem. Let $q(t)$ be the minimal polynomial of $a$ over $E_H$, with degree $m=[E\,\colon E_H]$. Recall that by the Divisibility Property (Gallian theorem 20.3), $q(t)$ divides any polynomial over $E_H$ that has $a$ as a root.

Let $H=\{\epsilon=\sigma_1,\sigma_2,\ldots,\sigma_h\}$, where $\epsilon$ is the identity automorphism. We want to prove that $h\ge m$. Consider the elementary symmetric functions using $\sigma_i(a)$ in place of $x_i$: $$ \alpha_1=\sum_{i=1}^h \sigma_i(a)\quad \alpha_2=\sum_{i< j} \sigma_i(a)\sigma_j(a)\quad\ldots\quad \alpha_j=\sum_{X\in{[h]\choose j}} \prod_{i\in X} \sigma_i(a)\quad\ldots \quad\alpha_h=\prod_{i=1}^h \sigma_i(a)$$ For convenience, let $\alpha_0=1$. Now we note that $$\sigma_k(\alpha_j)=\sum_{X\in{[h]\choose j}} \prod_{i\in X} (\sigma_k\circ\sigma_i)(a).$$ Since $H$ is a group, $\{\sigma_k\circ\sigma_i:i=1,\ldots,h\}$ is simply a permutation of $\{\sigma_1,\sigma_2,\ldots,\sigma_h\}$, and since $\alpha_j$ is symmetric in the $\sigma_i$, $\sigma_k(\alpha_j)=\alpha_j$. Hence, for all $j$, $\alpha_j\in E_H$. Now let $$p(t)=\prod_{i=1}^h (t-\sigma_i(a))=\sum_{i=0}^h (-1)^i\alpha_i t^{h-i}.$$ Since $\sigma_1(a)=a$, $p(a)=0$, and since $p(t)\in E_H[t]$, $q(t)$ divides $p(t)$. Since the degree of $q$ is $m$ and the degree of $p$ is $h$, $h\ge m$, as desired.

For the last statement of the theorem, let $H=G(E/F)$. Then by normality and parts (a) and (b), $[E\,\colon F]=[E\,\colon E_H]=|H|=|G(E/F)|$. $\qed$

Proof. Since the $a_i$ are roots of $f$, all $a_i$ are in the splitting field $E$. By the lemma on page 372 in Gallian, there is an isomorphism $\phi$ from $F(a_1)$ to $F(a_i)$ that takes $a_1$ to $a_i$ and fixes $F$. $E$ is the splitting field for $f$ over both $F(a_1)$ and $F(a_i)$, so by theorem 19.4 in Gallian, there is an automorphism $\sigma$ on $E$ that extends $\phi$—this $\sigma$ is the desired automorphism, and the proof of the lemma is complete. $\qed$

Proof. Suppose $E$ is a normal extension of $F$. As in the previous proof, let $E=F(a)$, $G(E/F)=\{\sigma_1,\sigma_2,\ldots,\sigma_n\}$, and $$p(t)=\prod_{i=1}^n (t-\sigma_i(a))=\sum_{i=0}^n (-1)^i\alpha_i t^{n-i},$$ where as before the $\alpha_i$ are the elementary symmetric functions in the $\sigma_i$. Since the $\alpha_i$ are fixed by $G(E/F)$, $\alpha_i\in F$ for every $i$. Thus, $p(t)\in F[t]$ and $p$ splits in $E$. Since $a$ is a root of $p$, $a$ must be in the splitting field of $p$, but since $E=F(a)$, this means $E$ is the splitting field of $p$.

Now, suppose $E$ is the splitting field for $f$ over $F$; we want to show that $E$ is a normal extension of $F$. The proof is by induction on $[E\,\colon F]$.

Base. If $[E\,\colon F]=1$, then $E=F$, $F$ is trivially the fixed field of $G(F/F)$ and so $E$ is a normal extension of $F$.

Induction step. The inductive hypothesis is:

If $E_1$ is an extension of $F_1$ with $[E_1\,\colon F_1]< [E\,\colon F]$, and $E_1$ is a splitting field over $F_1$, then $E_1$ is a normal extension of $F_1$.

Let $[E\,\colon F]=n>1$. The polynomial $f$ has an irreducible factor $p$ of degree $r>1$. By theorem 19.6 in Gallian, $p$ has distinct roots $a_1,\ldots,a_r$. Since $[E\,\colon F]=[E\,\colon F(a_1)][F(a_1)\,\colon F]$, $[E\,\colon F(a_1)]=[E\,\colon F]/[F(a_1)\,\colon F]=n/r < n$. Since $E$ is the splitting field of $f$ over $F(a_1)$, $E$ is a normal extension of $F(a_1)$, by the inductive hypothesis.

We need to show that the fixed field of $G(E/F)$ is $F$, that is, that if $a\in E$ is fixed by $G(E/F)$, then $a\in F$. Since $G(E/F(a_1))\le G(E/F)$, $a$ is fixed by $G(E/F(a_1))$ and so $a\in F(a_1)$ since $E$ is a normal extension of $F(a_1)$. By theorem 19.3 in Gallian, $$a=c_0+c_1a_1+c_2a_1^2+\cdots+c_{r-1}a_1^{r-1},$$ where the $c_i$ are in $F$. By lemma 1.3.3, for every $i$ there is a $\sigma_i\in G(E/F)$ such that $\sigma_i(a_1)=a_i$, so $$\sigma_i(a)=a=c_0+c_1a_i+c_2a_i^2+\cdots+c_{r-1}a_i^{r-1}.$$ Thus, every $a_i$ is a root of the polynomial $$(c_0-a)+c_1t+c_2t^2+\cdots+c_{r-1}t^{r-1}$$ of degree $r-1$. Since the $a_i$ are distinct, this implies that the coefficients of this polynomial are all 0, and in particular $a=c_0\in F$. $\qed$